Abstract
A very simple model of the process of maintaining balance by a person standing on a seesaw is considered. The model consists of a planar single-link inverted pendulum, which is connected by means of a cylindrical hinge, i.e., an “ankle joint”, to a support in the form of a segment of cylinder, whose axis is perpendicular to the pendulum. The support can oscillate by rolling on a horizontal surface, and the pendulum can oscillate in a plane that is perpendicular to the cylinder axis. The control is a torque applied on the axis of the hinge. This torque is assumed to have a restricted absolute value. A control law is constructed in the form of feedback along a single “unstable” coordinate of the open system in such a manner that the region of attraction of the linearized system would be the maximum possible. Several characteristic trajectories of the system for the control constructed are considered.
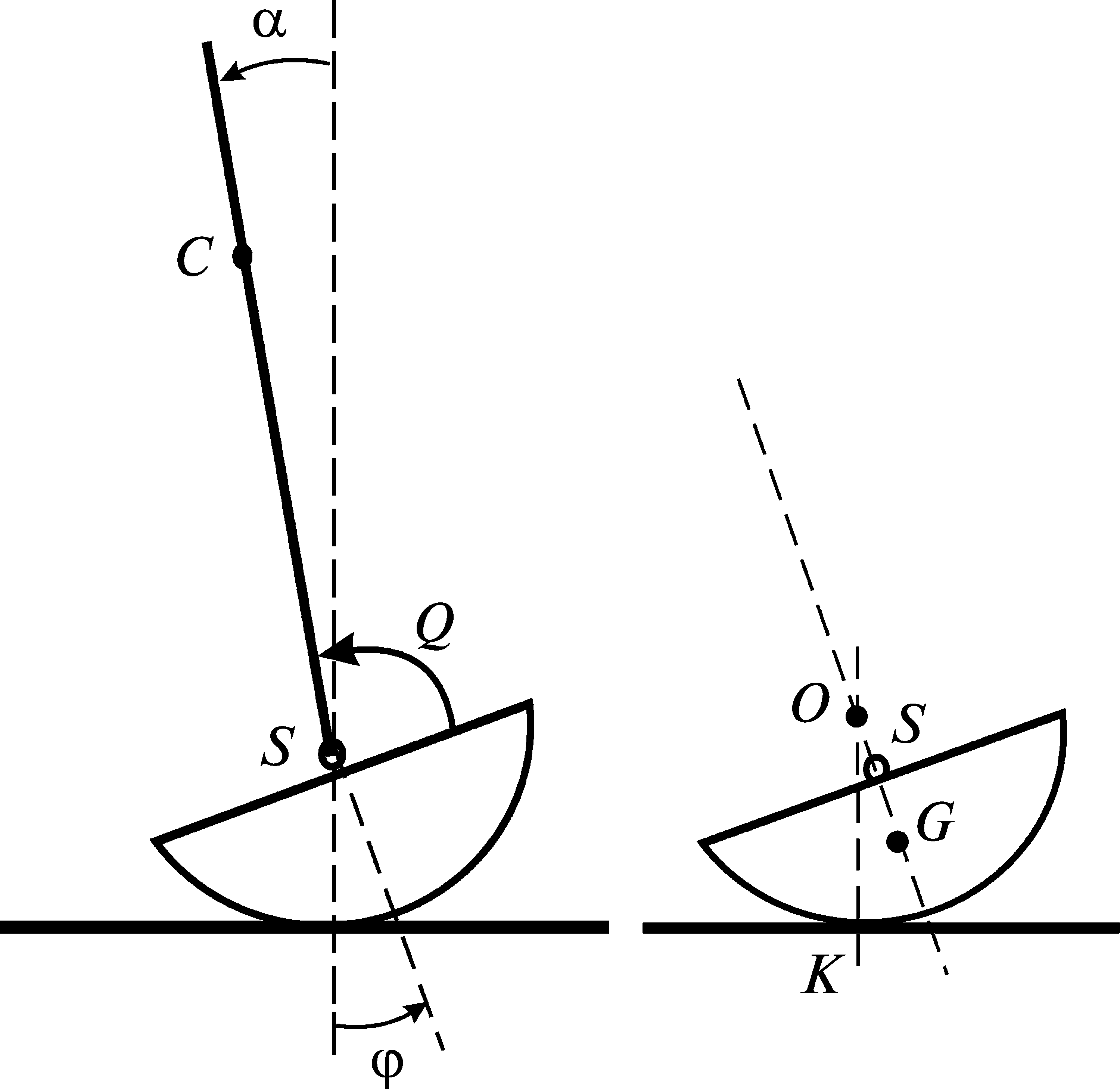
Mathematical models of the human motion that are intended for studying posture regulating processes must take into account that the maintenance of a human vertical posture is accomplished by applying control actions (torques) at the joints of the human extremities. Such models can be used in solving problems involving the synthesis of a control that minimizes a certain functional. The results of the solution of the optimization problem can be compared with the results of experiments. One of the motions that require such an analysis is the maintenance of balance by a person on the seesaw. It is a horizontal cylindrical segment, whose cylindrical surface is in contact with a horizontal plane. The corresponding test has become popular and is used in biomechanical investigations and in sports medicine.1–5 In this context, it would be interesting to select and investigate the optimal (in a certain sense) control for a mathematical model of the oscillations of a person on the seesaw.
In the first stage it would be expedient to consider the simplified model of the person oscillations in the sagittal plane. The person is modelled by a single-link inverted pendulum hinged to a horizontal cylindrical segment. The results of the tests in Ref. 6 enable us to assume that the motion in the sagittal plane when the person is balancing on the seesaw, at least for some people, may be described approximately using a similar model.